The following is a deliberately verbose explanation of the full collision resolution process, with friction, in 3 dimensions.
Note, there will be several different coordinate systems mentioned here, so unless otherwise stated it should be assumed that a given vector or matrix transformation lives in world coordinates.
The setup
As before, we are given two rigid bodies, say body0 and body1, which have collided. These rigid bodies have linear velocities 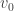 and
and 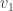 and angular velocities
and angular velocities 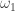 and
and  respectively, where the angular velocities are vectors oriented in the direction of rotation, with magnitude equal to radians/unit of time.
respectively, where the angular velocities are vectors oriented in the direction of rotation, with magnitude equal to radians/unit of time.
We also have contact data: an oriented contact normal  which points from body1 to body0 and represents the direction that body0 should be moved toward, and body1 away from, to resolve the penetration (This was a point of confusion, the book states that the contact normal would point from body0 to body1 by convention, but the actual math and code implementation clearly does the reverse). In addition, we have a point of contact vector
which points from body1 to body0 and represents the direction that body0 should be moved toward, and body1 away from, to resolve the penetration (This was a point of confusion, the book states that the contact normal would point from body0 to body1 by convention, but the actual math and code implementation clearly does the reverse). In addition, we have a point of contact vector  , and a positive depth of penetration scalar
, and a positive depth of penetration scalar  .
.
Finally, we have a coefficient of restitution  that defines the change in closing velocity. If the initial and final closing velocities in the direction of the contact normal are given as scalar values
that defines the change in closing velocity. If the initial and final closing velocities in the direction of the contact normal are given as scalar values  and
and  , then by definition:
, then by definition:

It is important to note that we define the closing velocity to be:
((instantaneous velocity of point p on rigid body 0) – (instantaneous velocity of point p on body 1))
in the direction of (dotted with) the contact normal  . That is, we subtract the 2nd body velocity. Since we only care about the resulting change in velocity, we could have oriented this the other way, and subtracted the first velocity instead, so long as the rest of the analysis used the same convention. Under this convention, a negative closing velocity means they are moving towards each other, and a positive closing velocity means they are separating. Remember
. That is, we subtract the 2nd body velocity. Since we only care about the resulting change in velocity, we could have oriented this the other way, and subtracted the first velocity instead, so long as the rest of the analysis used the same convention. Under this convention, a negative closing velocity means they are moving towards each other, and a positive closing velocity means they are separating. Remember  points away from body1 and toward body0.
points away from body1 and toward body0.
As before, our goal is to derive a formula that will take an impulse value  and convert it into a change in closing velocity in the direction of the contact normal
and convert it into a change in closing velocity in the direction of the contact normal  . From there we can invert the formula to find the necessary impulse to bring about the desired change in closing velocity based on the coefficient of restitution
. From there we can invert the formula to find the necessary impulse to bring about the desired change in closing velocity based on the coefficient of restitution  .
.
In the Collision Resolution 1 – resolving velocity post, we arrived at the following formula:
Formula 1: 
Where 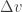 is the change in closing velocity, which is always measured in the direction of the contact normal
is the change in closing velocity, which is always measured in the direction of the contact normal  , and
, and  is the impulse, a scalar value, also in the direction of the contact normal
is the impulse, a scalar value, also in the direction of the contact normal  . Variables
. Variables  ,
,  , and
, and  correspond to the mass, moment of inertia in global coordinates, and the relative vector extending from the center of mass to the point of contact
correspond to the mass, moment of inertia in global coordinates, and the relative vector extending from the center of mass to the point of contact  , also in global coordinates, for each respective rigid body in the sum. So technically
, also in global coordinates, for each respective rigid body in the sum. So technically  ,
,  and
and  should have a subscript in the above formula, but I leave it out to avoid clutter.
should have a subscript in the above formula, but I leave it out to avoid clutter.
Noteworthy fact, the impulse  will ultimately be applied directly to body0, and an oppositely directed impulse,
will ultimately be applied directly to body0, and an oppositely directed impulse, 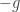 , to body1. With this, and the orientation of the contact normal in mind, we expect that the impulse scalar g (and likewise, the x component of the impulse vector g when working in 3 dimensions), will be positive, since it is, after all, the time integral of the forces in the direction of the contact normal, towards body0.
, to body1. With this, and the orientation of the contact normal in mind, we expect that the impulse scalar g (and likewise, the x component of the impulse vector g when working in 3 dimensions), will be positive, since it is, after all, the time integral of the forces in the direction of the contact normal, towards body0.
Our goal now, since we want to account for friction, is to convert Formula 1 into a matrix formula of the form:

Where the change in closing velocity 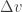 , and the impulse
, and the impulse  are now vectors given in contact coordinates. Remember in contact coordinates, the x axis is oriented in the direction of the contact normal
are now vectors given in contact coordinates. Remember in contact coordinates, the x axis is oriented in the direction of the contact normal  . The y and z axis can be somewhat arbitrary so long as they form a right handed coordinate system.
. The y and z axis can be somewhat arbitrary so long as they form a right handed coordinate system.
First let’s take a moment to review and re-derive Formula 1 before expanding it into 3 dimensions. 🙂
Re-deriving the results – Linear Impulse
Remember impulse is usually described as a change in linear momentum but I like to think of it slightly differently. Using Newton’s classic formula:

We can integrate both sides with respect to time, for some time duration under which an impact occurs:

The impulse then, can be thought of as a force integral over time. This concept is not much needed for linear impulse, but for angular impulse, it helps to think of it this way, which we’ll get to shortly.
Using the right side of the above equation, we easily see:

which is the linear component of Formula 1.
Re-deriving the results – Angular Impulse
First we need to review some of our angular rotation formulas in the context of the collision setup.
First, by definition of the inertia tensor:
Formula 2: 
Where  and
and 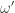 are torque and angular acceleration (as vectors in global coordinates) respectively, and
are torque and angular acceleration (as vectors in global coordinates) respectively, and  is the moment of inertia in global coordinates.
is the moment of inertia in global coordinates.
Likewise, we have a fairly intuitive formula to compute torque:
Formula 3: 
This formula makes a lot of intuitive sense if you consider the geometry:
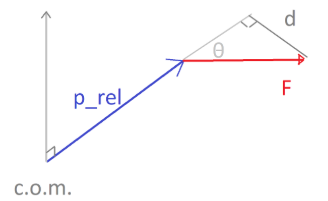
(Let’s not confuse d with the penetration depth, it only refers to the length of the triangle side indicated).
Recall that  is the vector extending from the center of mass to the point of contact p, at which the force
is the vector extending from the center of mass to the point of contact p, at which the force  is being applied. It makes complete sense that the direction of the torque vector would be normal to the plane defined by
is being applied. It makes complete sense that the direction of the torque vector would be normal to the plane defined by  and
and  . It also makes sense that the magnitude of the torque (arm length) * (normal force) would be
. It also makes sense that the magnitude of the torque (arm length) * (normal force) would be  where
where  is the angle between
is the angle between  and
and  .
.
Combining Formula 2 and Formula 3 by substitution for  we obtain:
we obtain:
Formula 4: 
Lastly, let’s assume that the force  is always along the direction of the contact normal
is always along the direction of the contact normal  be it positive or negative, and let
be it positive or negative, and let 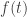 be the magnitude (and direction) of that force, such that:
be the magnitude (and direction) of that force, such that:
 .
.
If we treat  and
and  as constants over a time duration from
as constants over a time duration from 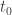 to
to 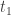 we can integrate Formula 4 with respect to time, to obtain:
we can integrate Formula 4 with respect to time, to obtain:

By pulling out constants, and taking advantage of the fact that cross products are distributive, we can simplify the formula as follows:

Taking note that  is a scalar value, and equal to
is a scalar value, and equal to  , we can pull it out to obtain the following formula:
, we can pull it out to obtain the following formula:
Formula 5: 
The quantity  is what’s sometimes called “Impulsive torque” for note its similarity to the torque formula in Formula 3 (especially if you combine
is what’s sometimes called “Impulsive torque” for note its similarity to the torque formula in Formula 3 (especially if you combine  and
and  to describe the impulse as a vector), and note how Formula 5 is analogous to Formula 4.
to describe the impulse as a vector), and note how Formula 5 is analogous to Formula 4.
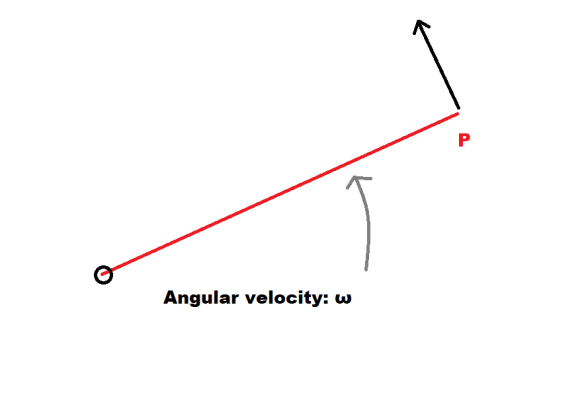
Linearizing the rotation:
We have a delta in angular velocity, but what linear velocity does that amount to at the point of contact? For this we have another geometrically intuitive result:
Formula 6: 
Where  is the linear velocity resulting from the rotation
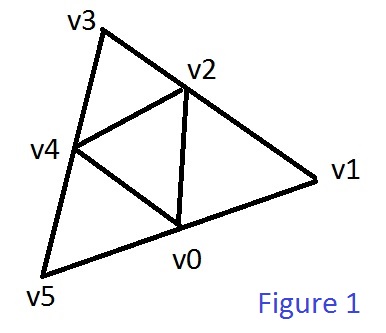
is the linear velocity resulting from the rotation  . Consider the following diagram to see why this makes intuitive sense:
. Consider the following diagram to see why this makes intuitive sense:
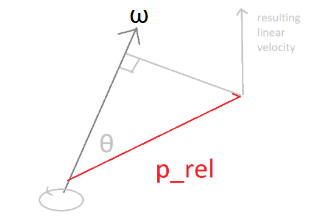
Recall that  is a vector and directed along the axis of rotation, it makes complete sense that the direction would be normal to the plane defined by
is a vector and directed along the axis of rotation, it makes complete sense that the direction would be normal to the plane defined by  and
and  . Moreover, the magnitude is given by:
. Moreover, the magnitude is given by:

Where 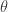 is the angle between
is the angle between  and
and  .
.
Lastly, we need the velocity in the direction of the contact normal. So we simply take the dot product with  to obtain the angular portion of the delta in closing velocity, which we call
to obtain the angular portion of the delta in closing velocity, which we call  :
:
Formula 7: 
Note we are sometimes using quantities like:  and
and  interchangeably, and similarly for linear velocities:
interchangeably, and similarly for linear velocities: 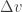 and
and  . Do not confuse the
. Do not confuse the  with an infinitesimal or a derivative, these are just differences, subtractions, and therefore the same theory holds. With this in mind, we can replace
with an infinitesimal or a derivative, these are just differences, subtractions, and therefore the same theory holds. With this in mind, we can replace  in Formula 7 with
in Formula 7 with  from Formula 5 to obtain:
from Formula 5 to obtain:
Formula 8: 
Note we took advantage of  being a scalar, and pulled it out in front.
being a scalar, and pulled it out in front.
Putting it all together:
Combining our linear velocity as a result of rotation, together with our earlier linear result, we obtain:
Formula 9: 
Note the dot product with  only applies to the angular component. The impulse scalar
only applies to the angular component. The impulse scalar  is already assumed to be in along the direction of the contact normal.
is already assumed to be in along the direction of the contact normal.
Finally, we need to determine the delta in closing velocity between the two bodies as a result of the impulse  . By our convention for closing velocity, we subtract the 2nd body (body1) velocity. However, the forces for the 2nd body are also oppositely directed and therefore the impulses are oppositely directed. Therefore, the negatives cancel and we simply add the two to obtain Formula 1:
. By our convention for closing velocity, we subtract the 2nd body (body1) velocity. However, the forces for the 2nd body are also oppositely directed and therefore the impulses are oppositely directed. Therefore, the negatives cancel and we simply add the two to obtain Formula 1:
Formula 1: 
Matrix Form
Formula 1 is a frictionless derivation that only accounts for the change in velocity along one direction. We review it because 1) it motivates the matrix derivation and 2) we will use this frictionless formula as a simplified model when resolving interpenetration.
We will use a similar derivation of Formula 1 to determine a matrix 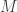 that transforms from an impulse
that transforms from an impulse  given in contact coordinates, to a delta in velocity,
given in contact coordinates, to a delta in velocity, 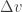 also given in contact coordinates. Once we are armed with this transformation, we will see how we use it to calculate a friction-based impulse.
also given in contact coordinates. Once we are armed with this transformation, we will see how we use it to calculate a friction-based impulse.
For this, we need to express the cross product as a matrix transformation. It turns out that for any vector  , we can find a corresponding matrix
, we can find a corresponding matrix  such that
such that  .
.
Now recall Formula 5:

Note this defined the change in angular velocity as a result of an impulse in the direction  scaled by the scalar
scaled by the scalar  . If we rename our variables to combine
. If we rename our variables to combine  and
and  into a single vector
into a single vector  , we can write the above formula as:
, we can write the above formula as:
Formula 5.1: 
Note that  was a vector in world coordinates and so in the above formula
was a vector in world coordinates and so in the above formula  would also be in world coordinates. We want things in contact coordinates ultimately, so we’ll address this in a bit.
would also be in world coordinates. We want things in contact coordinates ultimately, so we’ll address this in a bit.
Once again, we must linearize the rotation to determine the change in velocity at the point of contact. So, as before we use formula 6 (again noting we can interchange  and
and  ) and substitute our result from Formula 5.1 to obtain:
) and substitute our result from Formula 5.1 to obtain:
Formula 5.5: 
Recalling that we can reverse the order of a cross product by adding a negative sign we can rewrite this as:

Now, we can replace our cross products with  with the corresponding matrix
with the corresponding matrix  . Let’s just call it
. Let’s just call it 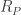 for short. (The book refers to this as a skew matrix, since it is skew symmetric). Moreover, since we are just dealing with matrices which are associative, we can regroup the parenthesis:
for short. (The book refers to this as a skew matrix, since it is skew symmetric). Moreover, since we are just dealing with matrices which are associative, we can regroup the parenthesis:
Formula 6.1: 
We are almost there. Both  and
and  are in world coordinates and we want our delta velocity AND our impulse to be in contact coordinates. So if we want
are in world coordinates and we want our delta velocity AND our impulse to be in contact coordinates. So if we want  in contact coordinates and we have a “contact to world” matrix
in contact coordinates and we have a “contact to world” matrix  , we must replace
, we must replace  in the formula above with
in the formula above with  . Moreover, we must convert the final result of the formula back to contact coordinates by left multiplying the result by
. Moreover, we must convert the final result of the formula back to contact coordinates by left multiplying the result by  . This results in the following:
. This results in the following:
Formula 7.1: 
Now comes the easy part! We have above what we call the “angular intertia”. Now we just need the “linear inertia”. Before we just scaled by  so in matrix world we just need a diagonal matrix
so in matrix world we just need a diagonal matrix  . Note this maps from contact coordinates to contact coordinates so no change of basis conversions are needed. So combining the linear and angular inertias, we obtain the total velocity delta in contact coordinates:
. Note this maps from contact coordinates to contact coordinates so no change of basis conversions are needed. So combining the linear and angular inertias, we obtain the total velocity delta in contact coordinates:
Formula 8.1: 
Finally, through the exact same reasoning as before, if we wish to account for the delta in closing velocity between two bodies (accounting for our closing convention of body0 velocity – body1 velocity, and the oppositely directed forces), we obtain the following sum:
Formula 9.1: 
From which we have finally derived our magical inertia matrix 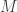 that converts from an impulse vector
that converts from an impulse vector  in contact coordinates to a change in closing velocity vector
in contact coordinates to a change in closing velocity vector 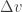 , also in contact coordinates:
, also in contact coordinates:
Formula 10: 
Armed with this now 3 dimensional mapping, we can compute the appropriate impulse that takes friction into account, in the next section!
Computing the impulse (with friction):
Recall that our general strategy for all of the velocity resolution is to compute the impulse; the impulse that will bring about the desired delta in velocity. Now that we have a 3 dimensional version, the x component of the closing velocity (in contact coordinates), will be determined by the coefficient of restitution, and the y,z components will be determined by the friction.
The trick the book uses is as follows:
1. Compute the impulse necessary to bring about the desired change in closing velocity in the direction of the contact normal  (the x axis of the contact coordinates) according to the restitution, and to completely kill the closing velocity in the
(the x axis of the contact coordinates) according to the restitution, and to completely kill the closing velocity in the  and
and  directions.
directions.
2. Check to see if there was enough friction present to stop the sliding, in which case the impulse computed by 1 is applied and we are done.
3. Otherwise, if there was not enough friction, we modify the impulse. We scale the impulse vector computed in step 1 in the yz plane only (we assume the yz direction of the modified impulse will be the same), and revise our x impulse, such that the friction equations are satisfied, and the delta in closing velocity along the contact normal (the x axis of the contact coordinates) is still what is dictated by the restitution.
Step 1:
If our initial closing velocity in contact coordinates is given by  and
and  is our restitution, then the desired change in closing velocity is given by:
is our restitution, then the desired change in closing velocity is given by:

So we therefore compute the correspond impulse  by solving the equation below (just take the matrix inverse):
by solving the equation below (just take the matrix inverse):

Step 2: So how much of an impulse do we have in the direction of the yz plane of the contact coordinate system, as a result of friction? Using the coefficient of friction  we have the classic formula:
we have the classic formula:
Formula 11: 
Where  and
and  are scalars. Once again, we can integrate the forces over a time duration to obtain an analogous formula of impulses:
are scalars. Once again, we can integrate the forces over a time duration to obtain an analogous formula of impulses:
Formula 12: 
By Pythagoras, and by noting that in our particular case  , and that
, and that  is the direction of the yz plane of the contact coordinates, we can apply the above formula to conclude the max frictional impulse:
is the direction of the yz plane of the contact coordinates, we can apply the above formula to conclude the max frictional impulse:
Formula 13: 
(Note we don’t need the absolute value of  because we expect
because we expect  to be positive, as mentioned before).
to be positive, as mentioned before).
Therefore, after computing  in step 1, we check to see if:
in step 1, we check to see if:
 is less than:
is less than: 
If this is so, then  is an appropriate impulse and we can apply it, and we are done!
is an appropriate impulse and we can apply it, and we are done!
Otherwise, we compute an entirely new impulse that has the following form:
Formula 14: 
Note what we have done here. We have used  only to deduce the yz direction of the new impulse, and then normalized and scaled it in the yz plane according to the friction relationship. We have also introduced a new variable
only to deduce the yz direction of the new impulse, and then normalized and scaled it in the yz plane according to the friction relationship. We have also introduced a new variable  . We are figuring out an entirely different impulse now, and
. We are figuring out an entirely different impulse now, and  is the only variable to solve for.
is the only variable to solve for.
Solving for it is actually quite easy. This modified impulse corresponds to a modified delta in closing velocity:
 .
.
We actually only know the x component of  , which is the delta in closing velocity based on the restitution, which let’s just call
, which is the delta in closing velocity based on the restitution, which let’s just call  to be concise. It turns out this is all we need. We substitute for both
to be concise. It turns out this is all we need. We substitute for both  and
and  in the equation above, to obtain:
in the equation above, to obtain:

(Note we are using a T exponent to denote transpose as the vectors should be vertical).
If we look at the very top row of this matrix equation, we can obtain a single, scalar value equation in one variable:
![\Delta v_f = M[0] g'_x + M[1]\mu g_x' \frac{{g_{kill}}_y}{\sqrt{({g_{kill}}_y)^2 + ({g_{kill}}_z)^2}} + M[2] \mu g_x' \frac{{g_{kill}}_z}{\sqrt{({g_{kill}}_y)^2 + ({g_{kill}}_z)^2}}](https://s0.wp.com/latex.php?latex=%5CDelta+v_f+%3D+M%5B0%5D+g%27_x+%2B+M%5B1%5D%5Cmu+g_x%27+%5Cfrac%7B%7Bg_%7Bkill%7D%7D_y%7D%7B%5Csqrt%7B%28%7Bg_%7Bkill%7D%7D_y%29%5E2+%2B+%28%7Bg_%7Bkill%7D%7D_z%29%5E2%7D%7D+%2B+M%5B2%5D+%5Cmu+g_x%27+%5Cfrac%7B%7Bg_%7Bkill%7D%7D_z%7D%7B%5Csqrt%7B%28%7Bg_%7Bkill%7D%7D_y%29%5E2+%2B+%28%7Bg_%7Bkill%7D%7D_z%29%5E2%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Where ![M[0],M[1],M[2]](https://s0.wp.com/latex.php?latex=M%5B0%5D%2CM%5B1%5D%2CM%5B2%5D&bg=ffffff&fg=333333&s=0&c=20201002) denote the first three elements of the first row of matrix M, respectively.
denote the first three elements of the first row of matrix M, respectively.
Solving for  we obtain:
we obtain:
Formula 15: ![g'_x = \frac{\Delta v_f}{M[0] + M[1]\mu \frac{{g_{kill}}_y}{\sqrt{({g_{kill}}_y)^2 + ({g_{kill}}_z)^2}} + M[2] \mu \frac{{g_{kill}}_z}{\sqrt{({g_{kill}}_y)^2 + ({g_{kill}}_z)^2}}}](https://s0.wp.com/latex.php?latex=g%27_x+%3D+%5Cfrac%7B%5CDelta+v_f%7D%7BM%5B0%5D+%2B+M%5B1%5D%5Cmu+%5Cfrac%7B%7Bg_%7Bkill%7D%7D_y%7D%7B%5Csqrt%7B%28%7Bg_%7Bkill%7D%7D_y%29%5E2+%2B+%28%7Bg_%7Bkill%7D%7D_z%29%5E2%7D%7D+%2B+M%5B2%5D%C2%A0+%5Cmu+%5Cfrac%7B%7Bg_%7Bkill%7D%7D_z%7D%7B%5Csqrt%7B%28%7Bg_%7Bkill%7D%7D_y%29%5E2+%2B+%28%7Bg_%7Bkill%7D%7D_z%29%5E2%7D%7D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Then using Formula 14, we can use  to compute the rest of the impulse, and we are done!
to compute the rest of the impulse, and we are done!
One final note – the approach of solving for the top row threw me the first time because I wondered “How do we know the rest of the equation is satisfied?”. The answer is “There is nothing to be satisfied”. We modify the impulse and  comes out to be, whatever it comes out to be. So long as the friction equations and the top row are satisfied, we are golden.
comes out to be, whatever it comes out to be. So long as the friction equations and the top row are satisfied, we are golden.
This concludes our discussion of velocity resolution.
Resolving Interpenetration
We already discussed the details of resolving penetration in a previous post: ““Collision Resolution 2 – resolving interpenetration” but a few newer details have come to light, and also for the sake of completeness I will review it here.
Recall that the general approach taken is to first determine the change in closing velocity
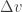 and then “fast forward time” by a time
and then “fast forward time” by a time  such that
such that  where
where  is the depth of penetration.
is the depth of penetration.
We will need our inertia formula (not to be confused with moment of inertia) we derived before to resolve the penetration. As briefly noted earlier, rather than use the friction-based 3×3 matrix, to work out this calculation, the book takes a simplified approach and use the frictionless Formula 1 (the friction version will be used for velocity resolution only). The formula is restated below:
Formula 1: 
Note that in this context, and for this discussion,  is a scalar again (though we will see shortly,
is a scalar again (though we will see shortly,  will be eliminated from our resulting formulas).
will be eliminated from our resulting formulas).
Let us refer to the entire sum in Formula 1 as  :
:

For the purpose of this discussion we are going to need to split the above sum into 4 pieces. Observe the left hand side of the formula is the linear component of the sum, and the right side is the angular component. Moreover, we have two rigid bodies, each of which contributed a linear and angular component to the sum.
To concisely denote these quantities, and to mimic the implementation code for ease of comparison, we will use standard programming language array notation with indices in brackets to denote which body we are using: [0] will correspond to body0 and [1] to body1.
Let us hereby define the following variables:
![linearInertia[0] = \frac{1}{m_0}](https://s0.wp.com/latex.php?latex=linearInertia%5B0%5D+%3D+%5Cfrac%7B1%7D%7Bm_0%7D&bg=ffffff&fg=333333&s=0&c=20201002)
![linearInertia[1] = \frac{1}{m_1}](https://s0.wp.com/latex.php?latex=linearInertia%5B1%5D+%3D+%5Cfrac%7B1%7D%7Bm_1%7D&bg=ffffff&fg=333333&s=0&c=20201002)
![angularInertia[0] = ( ( I_0^{-1}(p_{rel,0} \times n)) \times p_{rel,0} ) \cdot n](https://s0.wp.com/latex.php?latex=angularInertia%5B0%5D+%3D%C2%A0+%28+%28+I_0%5E%7B-1%7D%28p_%7Brel%2C0%7D+%5Ctimes+n%29%29+%5Ctimes+p_%7Brel%2C0%7D+%29+%5Ccdot+n&bg=ffffff&fg=333333&s=0&c=20201002)
![angularInertia[1] = ( ( I_1^{-1}(p_{rel,1} \times n)) \times p_{rel,1} ) \cdot n](https://s0.wp.com/latex.php?latex=angularInertia%5B1%5D+%3D%C2%A0+%28+%28+I_1%5E%7B-1%7D%28p_%7Brel%2C1%7D+%5Ctimes+n%29%29+%5Ctimes+p_%7Brel%2C1%7D+%29+%5Ccdot+n&bg=ffffff&fg=333333&s=0&c=20201002)
These should make some intuitive sense, for these are how we derived the closing velocities in the first place, by looking at the individual linear and angular inertia of each body before we combine them into a single sum. Note, however, that the inertia quantities above map an impulse to a change in velocity in the direction of the contact normal, but not a change closing velocity anymore, since we would need to compute differences for that. This is why we need this, we want to control for individual movements as we resolve the penetration between the two bodies.
So the question now is, how much time  would it take for the delta in closing velocity to cause the objects to separate by the penetration depth
would it take for the delta in closing velocity to cause the objects to separate by the penetration depth  ? Well:
? Well:

implies:

Set the right hand quantity equal to  and solve for
and solve for  to obtain:
to obtain:

So how much linear motion does this result in, for each object? For this let us introduce 4 new variables, similar to our approach for inertia:
![linearMove[0]](https://s0.wp.com/latex.php?latex=linearMove%5B0%5D&bg=ffffff&fg=333333&s=0&c=20201002)
![linearMove[1]](https://s0.wp.com/latex.php?latex=linearMove%5B1%5D&bg=ffffff&fg=333333&s=0&c=20201002)
![angularMove[0]](https://s0.wp.com/latex.php?latex=angularMove%5B0%5D&bg=ffffff&fg=333333&s=0&c=20201002)
![angularMove[1]](https://s0.wp.com/latex.php?latex=angularMove%5B1%5D&bg=ffffff&fg=333333&s=0&c=20201002)
These correspond to the linear shifts in the direction of the contact normal (be it positive or negative) that will be applied for each body. The angularMove quantities, it should be noted, are 1) not the actual rotation values, but the linear motion resulting from that rotation which will be applied, 2) linear approximations of an arc, and part of why we want these quantities to be small.
Now that we have suitable notation, we note that we can multiply an inertia quantity by  to find a delta in velocity. We can then multiply that delta in velocity by a time duration
to find a delta in velocity. We can then multiply that delta in velocity by a time duration  to find the resulting movement (we use both of these facts a lot in the derivations below, so be clear on this):
to find the resulting movement (we use both of these facts a lot in the derivations below, so be clear on this):
Formula 16: ![linearMove[0] = (linearInertia[0]g)t = d \frac{linearInertia[0]}{totalInertia}](https://s0.wp.com/latex.php?latex=linearMove%5B0%5D+%3D%C2%A0%28linearInertia%5B0%5Dg%29t+%3D+d+%5Cfrac%7BlinearInertia%5B0%5D%7D%7BtotalInertia%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Formula 17: ![angularMove[0] = (angularInertia[0]g)t = d \frac{angularInertia[0]}{totalInertia}](https://s0.wp.com/latex.php?latex=angularMove%5B0%5D+%3D%C2%A0%28angularInertia%5B0%5Dg%29t+%3D+d+%5Cfrac%7BangularInertia%5B0%5D%7D%7BtotalInertia%7D&bg=ffffff&fg=333333&s=0&c=20201002)
The formulas for ![linearMove[1]](https://s0.wp.com/latex.php?latex=linearMove%5B1%5D&bg=ffffff&fg=333333&s=0&c=20201002) , and
, and ![angularMove[1]](https://s0.wp.com/latex.php?latex=angularMove%5B1%5D&bg=ffffff&fg=333333&s=0&c=20201002) are analogous, but we must apply a negative sign since the forces would be oppositely directed for body1 (this is true even though we eliminated impulse from the formulas because the g in the initial t calculation would not have its sign inverted).
are analogous, but we must apply a negative sign since the forces would be oppositely directed for body1 (this is true even though we eliminated impulse from the formulas because the g in the initial t calculation would not have its sign inverted).
Next we must determine how much rotation angularMove[0] and angularMove[1] correspond to, but there is something we must do first. Recall that the quantities are linear approximations of an arc and they are only suitable if the arc is relatively short. Sometimes, depending on the inertia tensor and mass values, the calculated angularMove could be so high it would be a bad approximation. To handle this, our algorithm will cheat a bit, and check to see if the angular move value is above some calibrated threshold, and if so, transfer some of the angularMove over to the linearMove. Yes this distorts our original reasoning a bit, but it works. We’ll cover this in the “Avoiding excessive rotation” section shortly, but for now just be aware that the angular and linear move may be modified after they are calculated, and before they are applied to the rigid bodies.
Applying the motion:
Applying the linear move quantities (after the excessive rotation modifications) is straightforward. We simply add/subtract the appropriate linear move quantity multiplied by the contact normal to body0/body1 respectively.
The rotations are a bit trickier. We can compute our delta in angular velocity  from Formula 5 and multiply it by our earlier time duration
from Formula 5 and multiply it by our earlier time duration  . The only issue is our logic to avoid excessive rotation may have overridden the angular move values, which invalidates our time duration t (we didn’t need to recompute t for the modification to the linear move, because all we needed to know was the desired move distance, whereas we still need t to compute the change in rotation).
. The only issue is our logic to avoid excessive rotation may have overridden the angular move values, which invalidates our time duration t (we didn’t need to recompute t for the modification to the linear move, because all we needed to know was the desired move distance, whereas we still need t to compute the change in rotation).
We therefore need to recompute  based on our new angular move value. Let’s call it
based on our new angular move value. Let’s call it  . This calculation is straightforward, we use an equation we saw before and solve for different variables:
. This calculation is straightforward, we use an equation we saw before and solve for different variables:
![angularMove[0] = (angularInertia[0]g)t'](https://s0.wp.com/latex.php?latex=angularMove%5B0%5D+%3D%C2%A0%28angularInertia%5B0%5Dg%29t%27+&bg=ffffff&fg=333333&s=0&c=20201002)
Solve for  to obtain:
to obtain:
Formula 19: ![t' = \frac{angularMove[0]}{angularInertia[0]g}](https://s0.wp.com/latex.php?latex=t%27+%3D+%5Cfrac%7BangularMove%5B0%5D%7D%7BangularInertia%5B0%5Dg%7D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
Now we must use Formula 5 which we restate below:
Formula 5: 
We need only multiply the right hand side of Formula 5 by  to obtain our resulting rotation (note the
to obtain our resulting rotation (note the  cancels out):
cancels out):
Formula 20: ![\Delta \theta = I^{-1}(P_{rel} \times n )\frac{angularMove[0]}{angularInertia[0]}](https://s0.wp.com/latex.php?latex=%5CDelta+%5Ctheta+%3D+I%5E%7B-1%7D%28P_%7Brel%7D+%5Ctimes+n+%29%5Cfrac%7BangularMove%5B0%5D%7D%7BangularInertia%5B0%5D%7D&bg=ffffff&fg=333333&s=0&c=20201002)
Note that  really should be denoted as
really should be denoted as ![\Delta \theta[0]](https://s0.wp.com/latex.php?latex=%5CDelta+%5Ctheta%5B0%5D&bg=ffffff&fg=333333&s=0&c=20201002) and
and  as
as ![t'[0]](https://s0.wp.com/latex.php?latex=t%27%5B0%5D&bg=ffffff&fg=333333&s=0&c=20201002) since they each correspond to body0, but it seemed cleaner for this discussion to omit these. As before, the body1 result is analogous but we must multiply by -1 to account for the oppositely directed forces.
since they each correspond to body0, but it seemed cleaner for this discussion to omit these. As before, the body1 result is analogous but we must multiply by -1 to account for the oppositely directed forces.
Lastly this rotation vector would be applied to the orientation of the respective body by using an updateByVector() function on the quaternion, or something to that effect.
We will now discuss how to avoid the excessive rotation before giving a full summary of the penetration resolution process.
Avoiding Excessive rotation:
As usual, the book uses some odd motivational reasoning that does not quite agree with the implementation (at least in my mind).
The implementation takes the following approach:
1. Set a maximum rotation threshold given in radians, let’s call it  .
.
2. Use  to compute the corresponding maximum move at the point of contact.
to compute the corresponding maximum move at the point of contact.
3. See if the originally computed angularMove value exceeds this value, and if so, transfer some of the move over to the linear move.
Only step 2. really requires comment.
Imagine for a given relative contact vector  we applied a rotation of
we applied a rotation of  and wanted to know the corresponding linear movement at the point of contact in the direction of the contact normal
and wanted to know the corresponding linear movement at the point of contact in the direction of the contact normal  .
.
(This happens to be very similar to the “Law of Gearing” proof).
First we compute a “Projection” vector, by subtracting from  the component in the direction of
the component in the direction of  .
.

If we visualize the resulting right triangle, formed by  and the Projection vector, as a rigid body, we can see that the base of the 90 degree corner would have (approximately, for small rotations) the same shift
and the Projection vector, as a rigid body, we can see that the base of the 90 degree corner would have (approximately, for small rotations) the same shift  as the shift at the point of contact in the direction of the contact normal.
as the shift at the point of contact in the direction of the contact normal.
The shift and maximum allowable angular move would therefore be:

Finally, since  is usually calibrated as a small angle, we can approximate
is usually calibrated as a small angle, we can approximate  with
with  (also
(also  is constant, so it especially doesn’t matter). We therefore obtain the following formula found in the code implementation:
is constant, so it especially doesn’t matter). We therefore obtain the following formula found in the code implementation:
Formula 21:  .
.
Now let’s concisely summarize our algorithm and the appropriate formulas used.
Summary of penetration resolution:
Step 1: Compute the linearMove and angularMove values according to Formulas 16 & 17 (and the analogous formulas for body1), utilizing only the inertia quantities.
Step 2: Use formula 21 to see if the angularMove values are too high, and transfer the excess over to linearMove.
Step 3: Apply the linearMove shifts directly to the positions of the rigid bodies.
Step 4: compute the applied rotations using Formula 20 (and the analogous result for body1), utilizing only the angularMove and angularInertia quantities.
Independence of velocity & penetration resolution:
Note that our formulas for penetration resolution ended up not depending on the impulse value  . This is serendipitous, because it means we can resolve a collision independent of the velocity situation. There are some occasions, when a collision could occur, but the closing velocity may be positive. Under such a circumstance, we would not want to perform a velocity resolution, but we MAY want to resolve the penetration, and by the above observation, we may do so.
. This is serendipitous, because it means we can resolve a collision independent of the velocity situation. There are some occasions, when a collision could occur, but the closing velocity may be positive. Under such a circumstance, we would not want to perform a velocity resolution, but we MAY want to resolve the penetration, and by the above observation, we may do so.
CODE REVIEW:
The following code is cited from Ian Millington’s Github. I do not own this code:
All of the calculations should follow fairly closely the formulas that were presented. Keep in mind the corrections that were noted before, such as the contact normal not being oriented from body0 to body1 as the book stated.
Fortunately Ian Millington used your preferred matrix convention:
1. The matrix multiplication by a vector uses right multiplied by a vertical vector – producing a linear combination of the matrix columns.
2. The *= operator is overloaded to mean “right multiply by” so A *= B == A*B
3. The elements of the matrix are represented as a 1d array of length n*n and proceed in row order. i.e. M[0],M[1],M[2] correspond to the first
Resolving velocity:


Comments:
- On line 311 it says “Build the matrix to convert contact impulse to change in velocity in world coordinates” this threw me a bit. I thought “contact impulse” meant an impulse vector in contact coordinates, but I think it means to say “impulse as a result of the contact”. The associated matrix is a world-to-world mapping, and agrees with our derivations.
- In the formula for impulseContact.x on line 369, desiredDeltaVelocity corresponds to
 in Formula 15.
in Formula 15.
Resolving interpenetration:



is now a scalar, and the orientation can be represented with a scalar value
describing the rotation from its initial orientation. It still remains true that:
, and
are scalars now as well.
and
as living in 3D space and having a 0 z-component. The cross product, being normal to the 2 vectors will be in the z direction, but the z coordinate will still describe the appropriate, signed torque magnitude.
with
for short:
vector. With this we can write our next 2D formula:
in Formula 1, and integrating both sides over a time duration from
to
, we have:
for some constant unit vector
, by observing that cross products are distributive, and that dot products are also distributive, and since
and
are constants, we can factor out the left side and right side of the integral, so that we can integrate only over the time dependent values:
(which again, is a scalar), and the right hand integral is simply
(the impulse as a scalar. So we can rewrite the above equation as:
and the scalar impulse
into a single vector
(in the direction of
with with magnitude equal to
then we have:
to obtain the direction of the normal force, dotted this with the force vector and then multiplied by the torque arm length
which would cause a canceling effect, resulting in:
which we could write as:
is a 90 degree rotation matrix. Once again, we could take advantage of the dot product being distributive to pull out a time integral of force and arrive at a similar impulse formula:
then the speed of the tip of that vector is trivially:
.
.
with
in Formula 4 (recalling that we can use quantities like
and
interchangeably):
applied in the direction of the contact normal
. In formula 5 we see the resulting delta in velocity as a result of an arbitrary 2d impulse vector (in particular, the delta in velocity as a result of rotation).
with
where
is now a scalar, and substitute this in Formula 5 above we obtain:
:
from the right side of Formula 7):
with
where
is a scalar.
it takes to cross the angular move distance (not I use t’ instead of t only to agree with a previously used convention):
cancels and we obtain:
to apply it (no fancy quaternion functions needed).
is in world coordinates and so is the result – also note
is the linearized change in velocity, in no particular direction, caused by the rotation. It has not been dotted with the contact normal, which is what we want in the matrix version (we let the conversion back into contact coordinates at the end take care of that). Also we probably should have called the above
but we keep it as is for consistency with previous posts.
with
where
represents the contact to world matrix (remember this is a 2×2 matrix now). Likewise, we must left multiply our matrix by
to bring the final result back into contact coordinates.
, and remember we are using
as a shorthand for
which, I remind you, is a 2d vector in world coordinates.
represents a diagonal matrix with
along the diagonal.
is short for
,
when it comes to rotation.
is the initial closing velocity and
is the desired final velocity based on the restitution. That is, just enough change to kill the sliding.
to find the appropriate impulse to achieve this.
, if so we can apply the impulse and we are done, if not move on to step 4:
as before, only know we have only a y component instead of y and z components, so the normalized direction of
is simply
. So:
we obtain:
.
using the Formula 15.